1.9 KiB
1.9 KiB
📌 Questão 37
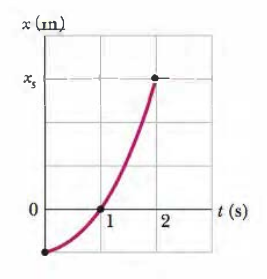
Fig. 2-26 mostra o movimento de uma partícula que se move ao longo do eixo x com aceleração constante. A escala vertical do gráfico é definida por x_s = 6.0\text{m}. Quais são
- O módulo da aceleração da partícula?
- E o sentido da aceleração da partícula?
📄 Solução 37.1
\begin{align*}
x(0) &= -2\text{m} \\
x(1) &= 0\text{m} \\
x(2) &= 6\text{m}
\end{align*}
\LARGE S_f = S_0 + v_0 \cdot t + \dfrac{a \cdot t^2}{2}
\begin{align*}
x(2) - x(0) &= \dfrac{a \cdot t^2}{2} \\
8\text{m} &= \dfrac{a \cdot t^2}{2} \\
8\text{m} &= a \cdot t^2 \cdot 2^{-1} \\
16\text{m} &= a \cdot t^2 \\
a &= 16\text{m} \cdot t^{-2} \\
a &= 16\text{m} \cdot 2^{-2} \\
a &= 4\text{m/s}^2 \\
\end{align*}
🧐 Resposta: $4m/s^2$ 🤯 Prova real:
\LARGE S_f = S_0 + v_0 \cdot t + \dfrac{a \cdot t^2}{2}
\begin{align*}
S_f &= -2m + \dfrac{a \cdot t^2}{2} \\
S_f &= -2m + \dfrac{4m/s^2 \cdot 1s^2}{2} \\
S_f &= -2m + \dfrac{4m}{2} \\
S_f &= -2m + 2m \\
S_f &= 0 \\
\end{align*}
📄 Solução 37.1
🧐 Resposta: Positivo
📌 Questão 42
Você está discutindo no telefone celular enquanto segue um carro de polícia não identificado, a 25 m de distância; os dois veículos estão a 110 km/h. A discussão distrai sua atenção do carro de polícia por 2,0 s (tempo suficiente para você olhar para o telefone e exclamar: "Eu me recuso a fazer isso!"). No início desses 2,0 s, o policial freia bruscamente, com uma desaceleração de 5,0 m/s^2
- Qual é a distância entre os dois carros quando você volta a prestar atenção no trânsito? Suponha que você leve outros
0,40 spara perceber o perigo e começar a frear. - Se você também freia com uma desaceleração de
5,0 m/s^2, qual é a velocidade do seu carro quando você bate no carro de polícia?